See also: Quadratic Equation Factorisation, Quadratic Equation Formula, Quadratic Equation Completing the Square, numbers

---

A quadratic function is a function defined by a second degree polynomial. It has the general form:

$$f\left(x\right)=a<!--\; InvisibleTimes\; -->x^2+b<!--\; InvisibleTimes\; -->x+c\text{, with}a\ne 0$$

A quadratic equation is a quadratic function that is equated to $0$. It has the general form:

$$a<!--\; InvisibleTimes\; -->x^2+b<!--\; InvisibleTimes\; -->x+c=0\text{, with}a\ne 0$$

---

The calculator below will calculate the Discriminant ($D$) and find the solutions (roots) of a quadratic equation.

---

Properties of quadratic functions and quadratic equations:

• The graph of a quadratic function is called a parabola.
  • The axis of symmetry of the parabola is the line $x=\frac{-b}{2<!--\; InvisibleTimes\; -->a}$ .
  • The coordinate of the vertex of the parabola is found by evaluating the function at the axis of symmetry, i.e. evaluating $f\left(x\right)$ at $x=\frac{-b}{2<!--\; InvisibleTimes\; -->a}$ .
  • If $a>0$ (i.e. positive), the parabola of the function will face (open) up.
    If $a<0$ (i.e. negative), the parabola of the function will face (open) down.
    
    
• The value of $b^2-4<!--\; InvisibleTimes\; -->a<!--\; InvisibleTimes\; -->c$ is called the Discriminant ($D$ or $\Delta$) of the quadratic equation.
  By looking at the value of the discriminant of a quadratic equation, we can know the following:
  
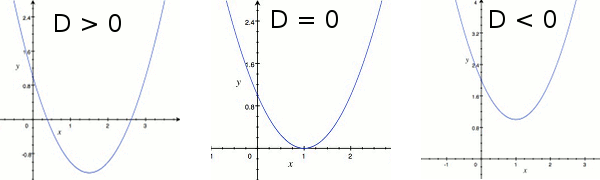
  • If the discriminant is positive ($D>0$), the quadratic equation has 2 distinct roots and both are real numbers. The parabola of the quadratic function intercepts the $x$-axis at two points.
  • If the discriminant is equal to zero ($D=0$), the quadratic equation has 1 root and it is a real number. The parabola of the quadratic function intercepts the $x$-axis at exactly one point.
  • If the discriminant is negative ($D<0$), the quadratic equation has 2 distinct roots and both are complex numbers. The parabola of the quadratic function does not intercept the $x$-axis.
  
  
  

Methods to solve or find the roots of a quadratic equation

There are a few methods to solve a quadratic equation, other than using the calculator above. The following are some of them.

• Factorisation
• Completing the square
• Formula

By Jimmy Sie

See also: Quadratic Equation Factorisation, Quadratic Equation Formula, Quadratic Equation Completing the Square, numbers

See also: numbers