Lihat juga: matriks, eliminasi Gauss-Jordan, Transformasi linier geometris

---

Gunakan kalkulator di bawah ini untuk mencari solusi dari sistem persamaan linier dengan 2, 3 ataupun sampai 10 variabel.

Lihat di bawah untuk belajar berbagai macam metode untuk menyelesaikan sistem persamaan linier.

---

Metode untuk menyelesaikan sistem persamaan linier

Paling sedikit ada lima cara / metode untuk mencari solusi sistem persamaan linier.

• Eliminasi
• Substitusi
• Grafik
• Matriks Invers
• Eliminasi Gauss/ Eliminasi Gauss-Jordan

Sebagai contoh, marilah kita coba untuk mencari solusi sistem persamaan linier dengan tiga variabel berikut ini

$$\{\begin{array}{rrrrrll}x& +& y& -& z& =1& \text{(1)}\\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}\\ -4<!--\; InvisibleTimes\; -->x& -& y+& 3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\end{array}$$

---

Metode eliminasi

Metode ini bekerja dengan care mengeliminasi (menghilangkan) variabel-variabel di dalam sistem persamaan hingga hanya satu variabel yang tertinggal.

Pertama-tama, lihat persamaan-persamaan yang ada dan coba cari dua persamaan yang mempunyai koefisien yang sama (baik positif maupun negatif) untuk variabel yang sama. Misalnya, lihat persamaan $\text{(1)}$ dan $\text{(3)}$. Koefisien untuk $y$ adalah $1$ dan $-1$ untuk masing-masing persamaan. Kita dapat menjumlah kedua persamaan ini untuk menghilangkan $y$ dan kita mendapatkan persamaan $\text{(4)}$.

$$\begin{gathered} \begin{array}{rrrrrll}x& +& y& -& z& =1& \text{(1)}\\ -4<!--\; InvisibleTimes\; -->x& -& y& +& 3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\end{array} \\ \text{------------------------}+ \\ \begin{array}{rrrrrll}-3<!--\; InvisibleTimes\; -->x& \phantom{+}& \phantom{0}& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}\end{array} \end{gathered}$$

Perhatikan bahwa persamaan $\text{(4)}$ terdiri atas variabel $x$ dan $z$. Sekarang kita perlu persamaan lain yang terdiri atas variabel yang sama dengan persamaan $\text{(4)}$. Untuk mendapatkan persamaan ini, kita akan menghilangkan $y$ dari persamaan $\text{(1)}$ dan $\text{(2)}$. Dalam persamaan $\text{(1)}$ dan $\text{(2)}$, koefisien untuk $y$ adalah $1$ dan $3$ masing-masing. Untuk menghilangkan $y$, kita kalikan persamaan $\text{(1)}$ dengan $3$ lalu mengurangkan persamaan $\text{(2)}$ dari persamaan $\text{(1)}$.

$$\begin{array}{rrrrrlll}x& +& y& -& z& =1& \text{(1)}& \text{× 3}\\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}& \end{array}$$
$$\begin{gathered} \begin{array}{rrrrrlll}3<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 3<!--\; InvisibleTimes\; -->z& =3& \text{(1)}& \\ 8<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->y& -& 6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}& \end{array} \\ \text{------------------------}- \\ \begin{array}{rrrrrlll}-5<!--\; InvisibleTimes\; -->x& \phantom{+}& \phantom{0<!--\; InvisibleTimes\; -->y}& +& 3<!--\; InvisibleTimes\; -->z& =2& \text{(5)}& \end{array} \end{gathered}$$

Dengan persamaan $\text{(4)}$ dan $\text{(5)}$, mari kita coba untuk menghilangkan $z$.

$$\begin{array}{rrrrrl}-3<!--\; InvisibleTimes\; -->x& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}& \text{× 3}\\ -5<!--\; InvisibleTimes\; -->x& +& 3<!--\; InvisibleTimes\; -->z& =2& \text{(5)}& \text{× 2}\end{array}$$
$$\begin{gathered} \begin{array}{rrrrrl}-9<!--\; InvisibleTimes\; -->x& +& 6<!--\; InvisibleTimes\; -->z& =6& \text{(4)}& \\ -10<!--\; InvisibleTimes\; -->x& +& 6<!--\; InvisibleTimes\; -->z& =4& \text{(5)}& \end{array} \\ \text{------------------------}- \\ \begin{array}{rrrrrl}\phantom{+01<!--\; InvisibleTimes\; -->}x& \phantom{+}& \phantom{0<!--\; InvisibleTimes\; -->z}& =2& \text{(6)}& \end{array} \end{gathered}$$

Dari persamaan $\text{(6)}$ kita dapatkan $x=2$. Sekarang kita bisa subtitusikan (masukkan) nilai dari $x$ ke persamaan $\text{(4)}$ untuk mendapatkan nilai $z$.

$$\begin{array}{rrrll}-3<!--\; InvisibleTimes\; -->\left(2\right)& +& 2<!--\; InvisibleTimes\; -->z& =2& \text{(4)}\\ -6& +& 2<!--\; InvisibleTimes\; -->z& =2& \\ & & 2<!--\; InvisibleTimes\; -->z& =2+6& \\ & & 2<!--\; InvisibleTimes\; -->z& =8& \\ & & z& =8÷2& \\ & & z& =4& \end{array}$$

Akhirnya, kita substitusikan (masukkan) nilai dari $x$ dan $z$ ke persamaan $\text{(1)}$ untuk mendapatkan $y$.

$$\begin{array}{rll}2+y-4& =1& \text{(1)}\\ y& =1-2+4& \\ y& =3& \end{array}$$

Jadi solusi sistem persamaan linier di atas adalah $x=2$, $y=3$, $z=4$.

---

Metode substitusi

Pertama-tama, marilah kita atur persamaan $\text{(1)}$ ssupaya hanya ada 1 variabel di sebelah kiri.

$$\begin{array}{rl}x=1-y+z& \text{(1)}\end{array}$$

Sekarang kita substitusi $x$ ke persamaan $\text{(2)}$.

$$\begin{array}{rll}8<!--\; InvisibleTimes\; -->\left(1-y+z\right)+3<!--\; InvisibleTimes\; -->y-6<!--\; InvisibleTimes\; -->z& =1& \text{(2)}\\ 8-8<!--\; InvisibleTimes\; -->y+8<!--\; InvisibleTimes\; -->z+3<!--\; InvisibleTimes\; -->y-6<!--\; InvisibleTimes\; -->z& =1& \\ -5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->z& =1-8& \\ -5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->z& =-7& \text{(4)}\end{array}$$

Dengan cara yang sama seperti di atas, substitusi $x$ ke persamaan $\text{(3)}$.

$$\begin{array}{rll}-4<!--\; InvisibleTimes\; -->\left(1-y+z\right)-y+3<!--\; InvisibleTimes\; -->z& =1& \text{(3)}\\ -4+4<!--\; InvisibleTimes\; -->y-4<!--\; InvisibleTimes\; -->z-y+3<!--\; InvisibleTimes\; -->z& =1& \\ 3<!--\; InvisibleTimes\; -->y-z& =1+4& \\ 3<!--\; InvisibleTimes\; -->y-z& =5& \text{(5)}\end{array}$$

Sekarang kita atur persamaan $\text{(5)}$ supaya hanya ada 1 variabel di sebelah kiri.

$$\begin{array}{rl}z=3<!--\; InvisibleTimes\; -->y-5& \text{(5)}\end{array}$$

Kemudian, substitusi nilai dari $z$ ke persamaan $\text{(4)}$.

$$\begin{array}{rll}-5<!--\; InvisibleTimes\; -->y+2<!--\; InvisibleTimes\; -->\left(3<!--\; InvisibleTimes\; -->y-5\right)& =-7& \text{(4)}\\ -5<!--\; InvisibleTimes\; -->y+6<!--\; InvisibleTimes\; -->y-\mathrm{10}& =-7& \\ y& =-7+10& \\ y& =3& \end{array}$$

Sekarang kita sudah tahu nilai dari $y$, kita dapat masukkan nilai ini ke persamaan $\text{(5)}$ untuk mencari $z$.

$$\begin{array}{rll}z& =3<!--\; InvisibleTimes\; -->\left(3\right)-5& \text{(5)}\\ z& =9-5& \\ z& =4& \end{array}$$

Akhirnya, kita substitusikan nilai dari $y$ and $z$ ke persamaan $\text{(1)}$ untuk mendapatkan nilai $x$.

$$\begin{array}{rll}x& =1-3+4& \text{(1)}\\ x& =2& \end{array}$$

---

Metode grafik

Penyelesaian sistem persamaan linier dengan metode grafik dilakukan dengan cara menggambar garis garis atau bidang planar yang merupakan representasi dari persamaan-persamaan yang ada dalam sistem tersebut. Solusinya adalah koordinat-koordinat yang merupakan titik potong dari garis-garis ataupun bidang-bidang planar itu.

Sebagai contoh, marilah kita lihat sistem persamaan liniear dengan dua variabel berikut ini.

$$\{\begin{array}{rrrr}x& +& y& =3\\ 2<!--\; InvisibleTimes\; -->x& -& y& =-3\end{array}$$

Gambar kedua garis dari persamaan-persamaan di atas.

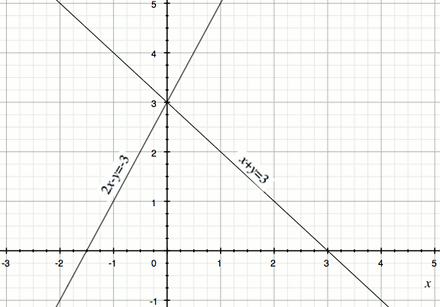
Seperti terlihat pada grafik di atas, kedua garis itu bertemu (mempunyai titik potong) pada titik $(0,3)$. Ini adalah solusi dari sistem persamaan linier tersebut, yaitu $x=0$, $y=3$.

Untuk persamaan linier dengan tiga variabel, solusinya adalah titik pertemuan dari tiga bidang planar dari masing-masing persamaan.

---

Metode Matriks Invers

Sistem persamaan linier yang terdiri atas persamaan-persamaan $\text{(1)}$, $\text{(2)}$ dan $\text{(3)}$ di atas dapat juga ditulis dengan bentuk notasi matriks sebagai berikut

$$\begin{array}{rl}AB& =C\\ \left(\begin{array}{rrr}1& 2& -1\\ 8& 3& -6\\ -4& -1& 3\end{array}\right)<!--\; InvisibleTimes\; -->\left(\begin{array}{c}x\\ y\\ z\end{array}\right)& =\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\end{array}$$

Solusinya adalah matriks $B$. Agar kita dapat mengisolasi $B$ sendirian di salah satu sisi dari persamaan di atas, kita kalikan kedua sisi dari persamaan di atas dengan invers dari matriks $A$.

$$\begin{array}{rl}{A}^{-1}AB& =A^{-1}C\\ B& =A^{-1}C\end{array}$$

Sekarang, untuk mencari $B$ kita perlu mencari $A^{-1}$. Silakan melihat halaman tentang matriks untuk belajar bagaimana mencari invers dari sebuah matriks.

$$\begin{array}{rl}{A}^{-1}& =\left(\begin{array}{rrr}-3& 2& 3\\ 0& 1& 2\\ -4& 3& 5\end{array}\right)\\ B& =\left(\begin{array}{rrr}-3& 2& 3\\ 0& 1& 2\\ -4& 3& 5\end{array}\right)<!--\; InvisibleTimes\; -->\left(\begin{array}{c}1\\ 1\\ 1\end{array}\right)\\ B& =\left(\begin{array}{c}2\\ 3\\ 4\end{array}\right)\end{array}$$

Jadi solusinya adalah $x=2$, $y=3$, $z=4$.

Metode ini dapat digunakan untuk menyelesaikan sistem persamaan linier dengan $n$ variabel. Kalkulator di atas juga menggunakan metode ini untuk menyelesaikan sistem persamaan linier.

---

Eliminasi Gauss / Eliminasi Gauss-Jordan

Sistem persamaan liniear yang terdiri atas persamaan-persamaan $\text{(1)}$, $\text{(2)}$ dan $\text{(3)}$ dapat juga dinyatakan dalam bentuk matriks teraugmentasi seperti berikut

$$A=\left(\begin{array}{rrrrr}1& 1& -1& \text{|}& 1\\ 8& 3& -6& \text{|}& 1\\ -4& -1& 3& \text{|}& 1\end{array}\right)$$

Dengan melakukan serangkaian operasi baris (Eliminasi Gauss), kita dapat menyederhanakan matriks di atas untuk menjadi matriks Eselon-baris.

$$A=\left(\begin{array}{rccll}1& 0.375& -0.75& \text{|}& 0.125\\ 0& 1& -0.4& \text{|}& 1.4\\ 0& 0& 1& \text{|}& 4\end{array}\right)$$

Kemudian kita bisa substitusikan kembali nilai-nilai yang kita dapat untuk mencari nilai dari semua variabel. Atau, kita juga bisa meneruskan dengan serangkaian operasi baris lagi sehingga matriks di atas menjadi matriks yang Eselon-baris tereduksi (dengan menggunakan Eliminasi Gauss-Jordan).

$$A=\left(\begin{array}{rrrrr}1& 0& 0& \text{|}& 2\\ 0& 1& 0& \text{|}& 3\\ 0& 0& 1& \text{|}& 4\end{array}\right)$$

Dengan melakukan operasi Eliminasi Gauss-Jordan, kita mendapatkan solusi dari sistem persamaan linier di atas pada kolom terakhir: $x=2$, $y=3$, $z=4$.

Untuk melihat secara mendetil operasi baris yang diperlukan, silakan melihat halaman tentang Eliminasi Gauss-Jordan.

By Jimmy Sie

See also: matrix, Gauss-Jordan elimination, Geometric Linear Transformation